入試で数学Ⅰを出題範囲としている大学や専門学校では、間違いなく出題されるであろう2次関数。
今回はその基礎である、一般形やグラフについて抑えていきましょう。
Contents
1次関数・2次関数の一般形
復習がてら、1次関数の一般形も紹介します。
1次関数の一般形
- $y=ax+b$ $a(\neq0), b$ は定数
続いて、2次関数の一般形を紹介します。
2次関数の一般形
- $y=ax^2+bx+c$ $a(\neq0), b, c$ は定数
1次関数・2次関数のグラフ
1次関数
傾き $a$ が正なら右肩上がり、負なら右肩下がりです。
切片 $b$ は $y$ 軸との交点です。
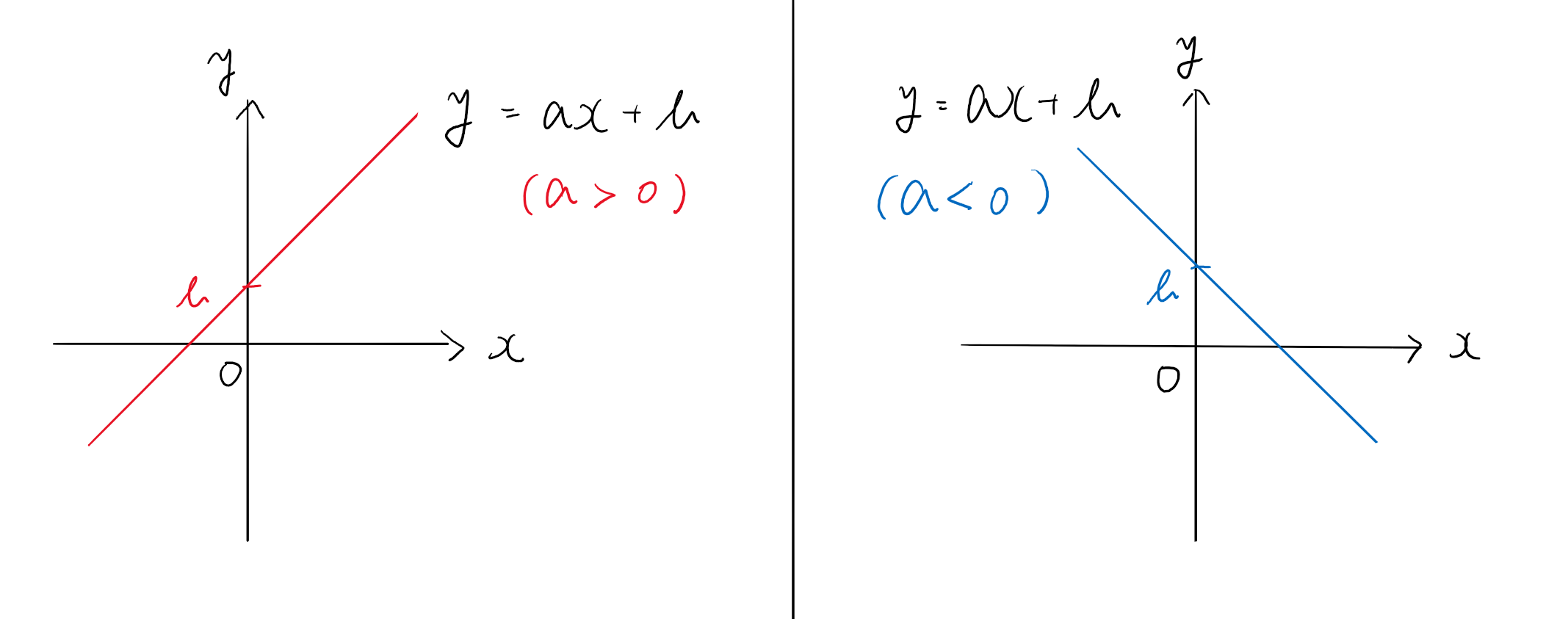
2次関数 $y=ax^2$
- 放物線:$y=ax^2$ のグラフと同じ形の曲線
- 軸:放物線が左右対称となる直線($x=定数$ の形で表せる)
- 頂点:放物線と軸の交点
$y=ax^2$ であれば、軸は $y$ 軸と一致し、頂点は原点と一致します。
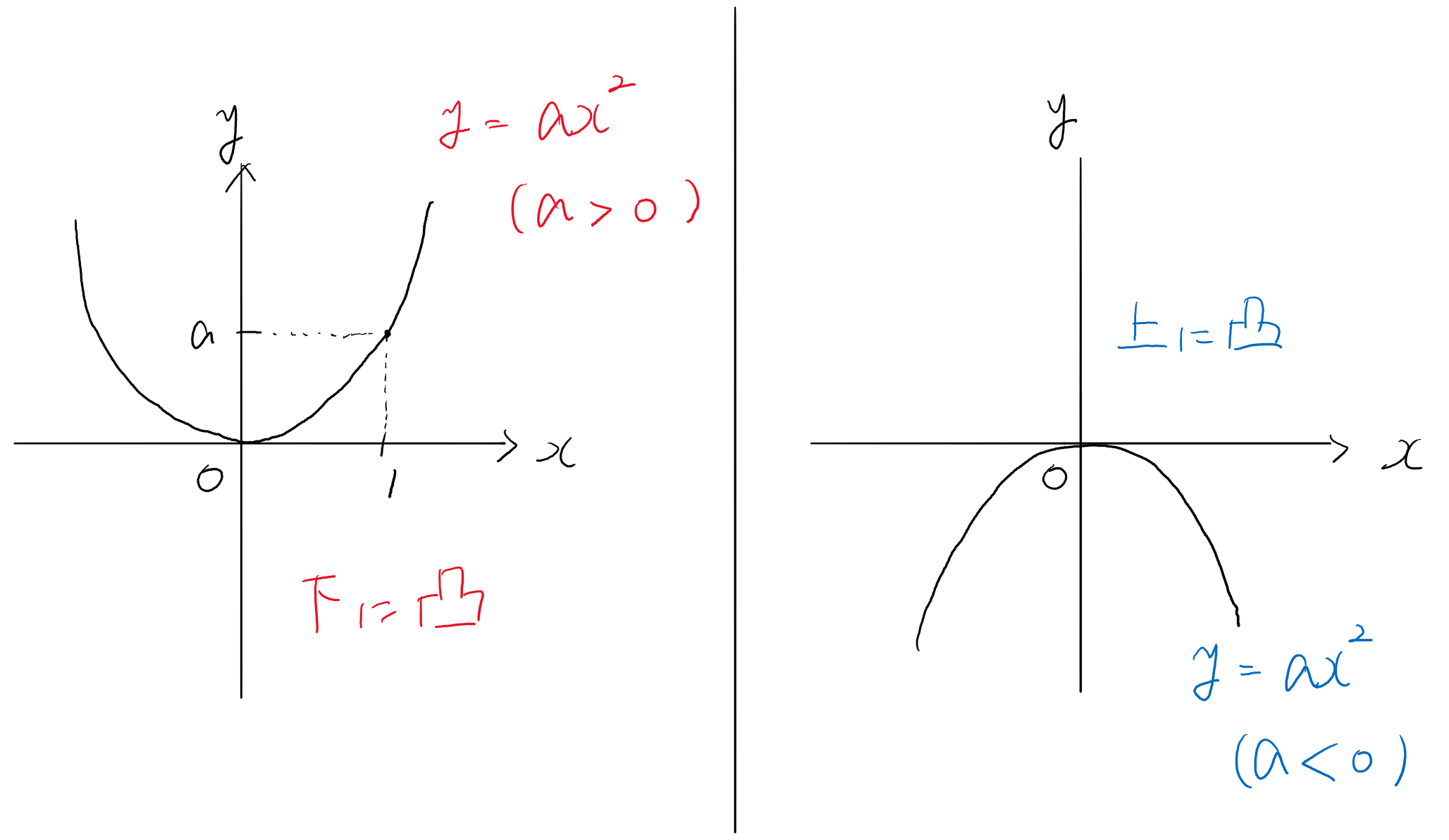
2次関数 $y=ax^2+bx+c$
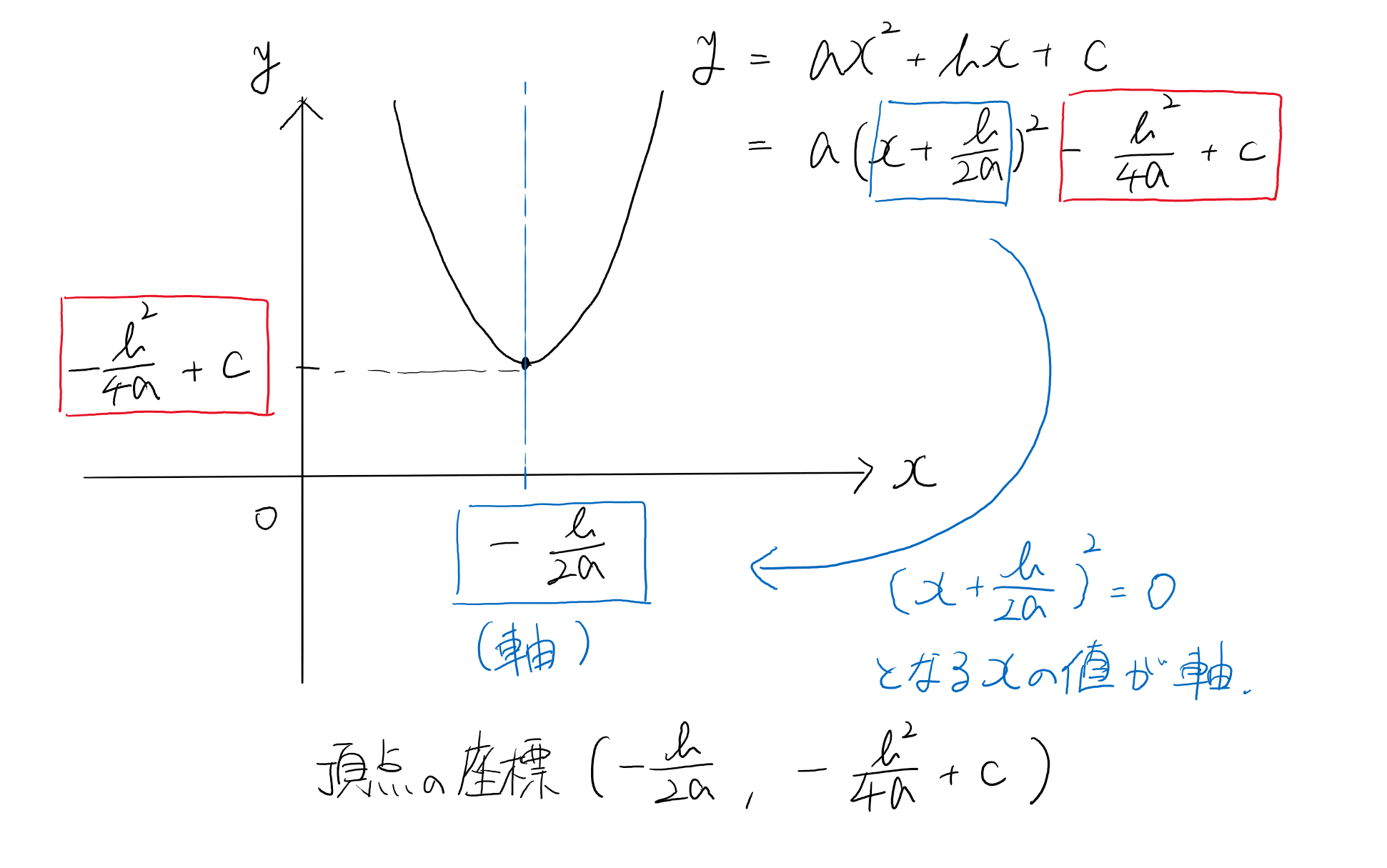
$y=ax^2+bx+c$ を平方完成すると…
$\begin{eqnarray}
y &=& ax^2+bx+c \\
&=& a(x^2+\frac{b}{a}x)+c \\
&=& a(x+\frac{b}{2a})^2-\frac{b^2}{4a^2}+c
\end{eqnarray}$
これをグラフに表すと、こんな感じです。
(今回は、グラフの頂点が第一象限へ来るように描きました。)
グラフの平行移動
- $y=f(x)$ を $x$ 軸方向へ $p$ 平行移動すると $y=f(x-p)$
- $y=f(x)$ を $y$ 軸方向へ $q$ 平行移動すると $y-q=f(x)$
グラフの対称移動
- $y=f(x)$ を $x$ 軸で対称移動すると $-y=f(x)$
- $y=f(x)$ を $y$ 軸で対称移動すると $y=f(-x)$
- $y=f(x)$ を 原点で対称移動すると $-y=f(-x)$
2次関数の点対称移動
- 頂点は頂点に移る
- $x^2$ の係数は $\pm$ が逆転する
過去問演習
準備中
ABOUT ME