超頻出問題「2次関数の最大値と最小値を求めよ」に用いる考え方です。
必ず ”軸” の位置に着目
”2次関数は軸に左右対象である放物線”ということを、前回の公式集にてお伝えしました。

【公式集】§3-1. 2次関数のグラフについて(一般形やグラフの平行移動・対称移動)入試で数学Ⅰを出題範囲としている大学や専門学校では、間違いなく出題されるであろう2次関数。
今回はその基礎である、一般形やグラフに...
2次関数の最大値・最小値を求める問題では、定義域が設けられる場合があります。
定義域が設定されている場合、軸の位置によって最大値・最小値が異なる場合があります。
なので、軸が未知数(例えば定数 $a$ など)の場合は、場合分けをする必要があります。
- 最大値・最小値は、”定義域”と”軸”の位置関係を考える
最大値・最小値の求め方
定義域が設定されていない場合
2次関数の最大値・最小値を求める際に、先ず確認すべきは「グラフが上に凸か、下に凸か」です。
先ずは、定義域が設定されていない場合を考えましょう。
例 $y=f(x)=ax^2+bx+c$ なら…
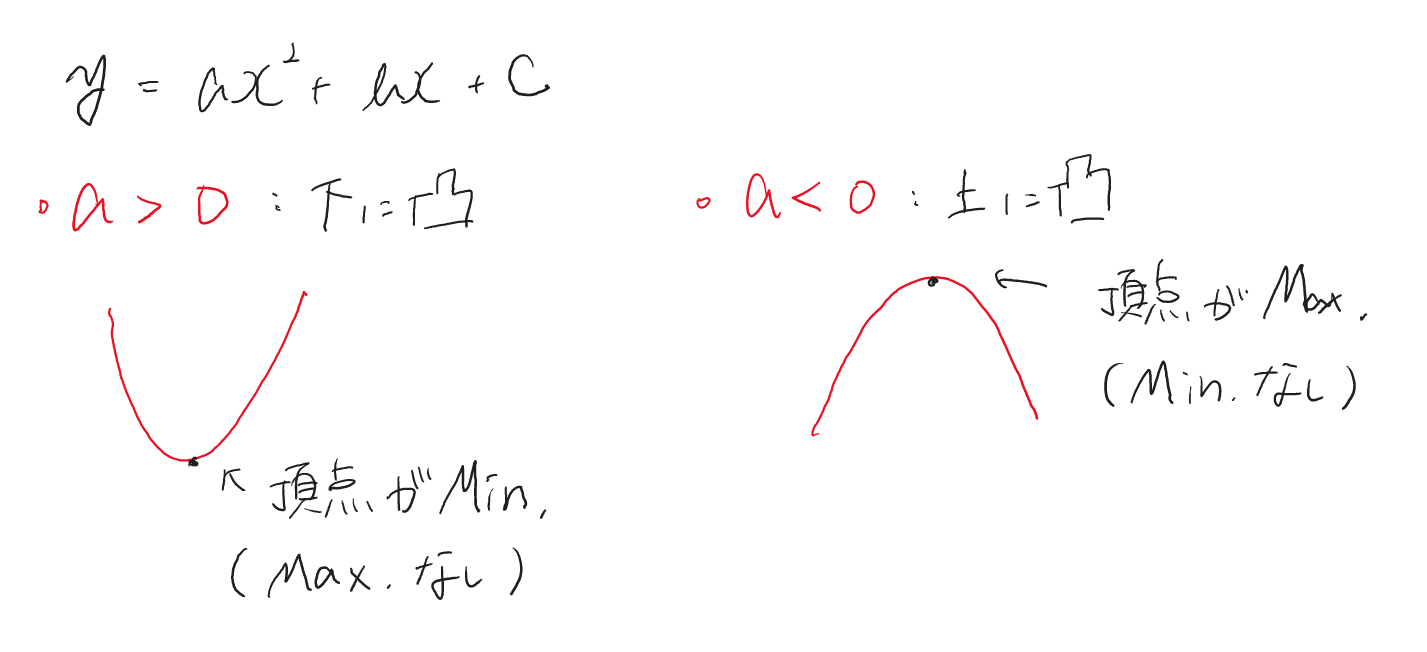
定義域が設定されている場合
もし定義域が設定されているなら、その定義域内における最大値・最小値を考えます。
例 $y=f(x)=x^2-8x+15$ $(0\leqq x\leqq 10)$ なら…
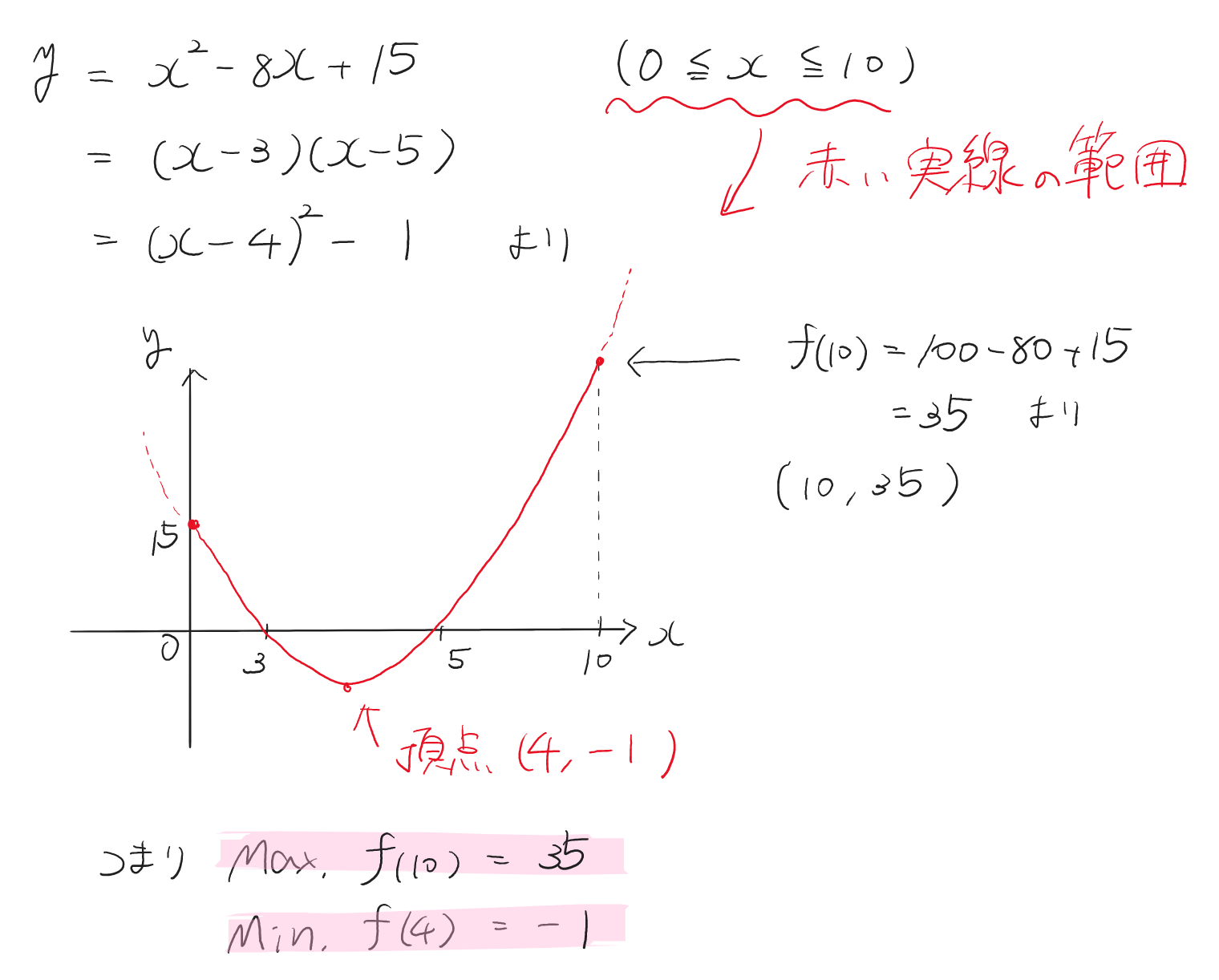
- 最大値・最小値は、グラフを描いて大小関係を考える
※当ブログでは今後、最大値を「Max.」・最小値を「Min.」と書くことがあります。
後は実際に問題を解いて、慣れていきましょう!
過去問演習
準備中
ABOUT ME