展開の公式を覚えておかないと、因数分解の問題を解くのは非常に大変です。
今回の公式集では、因数分解のコツについても触れていきます。
展開の公式
前回の公式集でも触れましたが、展開とは”整式の積を単項式の和にすること”です。

展開の公式はこんな感じです。
2次式…
- $(a\pm b)^2=a^2\pm 2ab+b^2$
- $(a+b)(a-b)=a^2-b^2$
- $(x+a)(x+b)=x^2+(a+b)x+ab$
- $(ax+b)(cx+d)=acx^2+(ad+bc)x+bd$
3次式…
- $(a\pm b)^3=a^3\pm 3a^2b+3ab^2\pm b^3$
- $(a\pm b)(a^2\mp ab+b^2)=a^3\pm b^3$
特に、3次式は符号の入れ替わりに注意してください。
因数分解の公式
因数分解とは、1つの整式を1次以上の整式の積で表すことです。
因数とは、もとの式を因数分解してできた整式の積を作っている各式のことです。
例 $x^2+7x+12$ を因数分解すると…
$x^2+7x+12=(x+3)(x+4)$
つまり、因数分解した整式の積を展開すると、もとの整式に戻るということです。
なので、基本的には展開の公式を覚えておけば、因数分解の公式は"その逆"をやればよいわけです。
基本の公式は、展開の公式を参照ください。
因数分解のコツ
因数分解のコツは、共通な因数(共通因数)を見つけることです。
例 $AB+AC$ を因数分解するなら…
各項の共通因数はAなので、Aでくくると
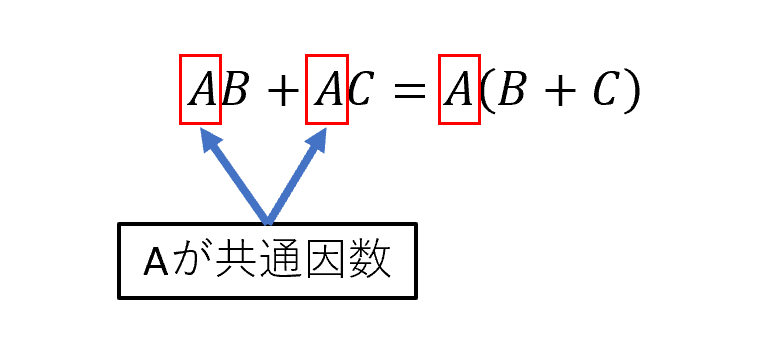
※ここでの「くくる」とは「共通因数をかっこの外に括(クク)りだす」という意味です。
一つにまとめる。ひとまとまりにする。「数式a+bを括弧で―・る」
もし共通因数を探しても見つからなかったら、共通因数を作るのも一つのテクニックです。また、式中の一部を一つのまとまりとして見るのもテクニックです。
この辺は実際の過去問演習でお話します。
困ったら"たすき掛け"の公式
- たすき掛けの公式
展開の公式より $acx^2+(ad+bc)x+bd=(ax+b)(cx+d)$ です。
$x^2$の係数と定数項に着目し、これを以下のように分解してみます。
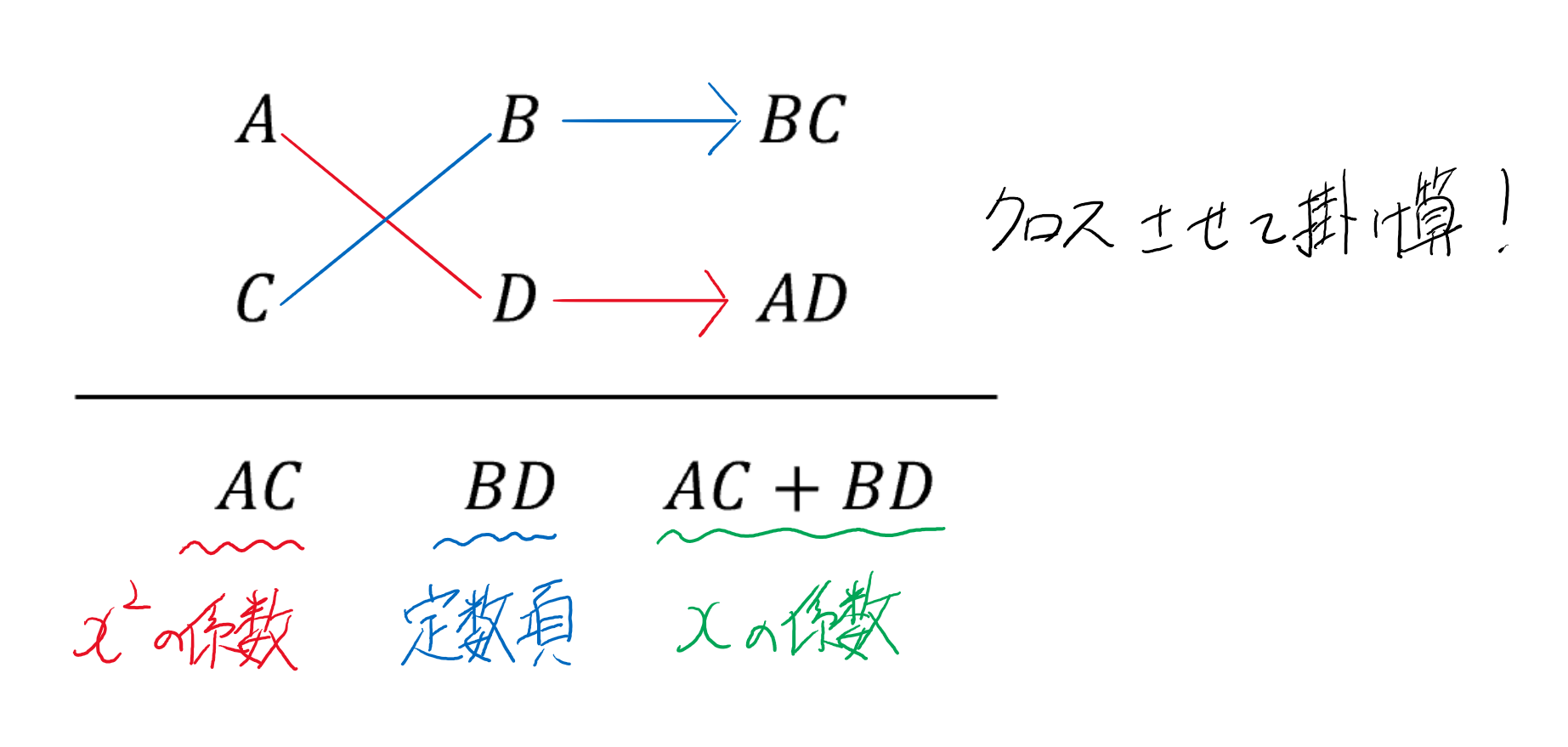
これが俗に言う"たすき掛けの公式"です。
$x^2$ の係数が $AC$ 、定数項が $BD$ となるので、それぞれの約数の積を考えればよいわけです。
例 $3x^2+17x+10$ を、たすき掛けの公式を用いて因数分解すると…

あとはもう慣れですので、ひたすら練習しましょう。
過去問演習
準備中