前回の公式集で、整式などの用語について触れました。

【公式集】§1-1.単項式・多項式・定数項などの用語を理解しよう高校数学で最初に教わるであろう分野から公式集を作っていきます。
今回は、単項式・多項式・定数項などの用語についてです。
そも...
今回から実際によく用いる公式に触れていきます。
整式の加法・減法について
2つの整式 $A$, $B$ について
- $A+B$ :同類項の係数をそのまま足してまとめる
- $A-B$ :$A+(-B)$ と考えて上記と同様に計算する
例 $A=x^3+2x^2+1$, $B=2x^3-5x+4$ とすると
$A+B$ は…
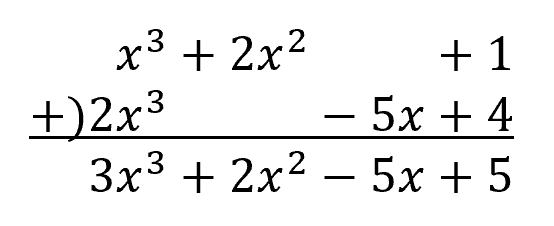
といった感じで計算をします。筆算とやっていることは変わらないですね。
計算ミスをしないように筆算をするポイントは、同類項を上下にきちんと揃えることです。
ちなみに…
$m, n$ を実数とすると
- $mA+nA=(m+n)A$
- $mA-nA=(m-n)A$
対称式について
- 対称式:文字を入れ替えても意味が変わらない式
- 必ず基本対称式($x,y$なら$x+y,xy$)で表せる
例 $x^2+y^2$ を $x+y,xy$ を用いて表すと…
$x^2+y^2=(x+y)^2-2xy$
整式の乗法について
単項式の乗法(指数法則)
そのうち数学Ⅱで指数関数をやりますが、指数法則を知らずに高校数学を勉強するのは厳しいです。最初のうちに公式集へ追加してください。
$a^n$ ($a$の$n$乗) :$a$を($1$に)$n$個掛けたもの、$n$を指数と呼ぶ
ーーーーーーーーーー
$m, n$を整数とすると
- $a^m×a^n=a^{m+n}$
- $a^m÷a^n=a^{m-n}$
- $(a^m)^n=a^{mn}$
- $(ab)^n=a^nb^n$
- $a^0=1$
$a^0=1$ に関しては、$a$を($1$に)$0$個掛けていると考えます。
展開の概念? 分配法則について
整式$A, B, C$において分配法則が成り立つ
- $A(B+C)=AB+AC$
- $(A+B)C=AC+BC$
つまり、次の法則も成り立つ($D$ も整式)
- $(A+B)(C+D)=AC+AD+BC+BD$
ーーーーーーーーーー
展開:整式の積を単項式の和にすること
例 $4x(3x^2+4y)=12x^3+16xy$
展開の公式については、次の公式集で触れます。

【公式集】§1-3.整式の展開と因数分解|たすき掛けの公式とコツ展開の公式を覚えておかないと、因数分解の問題を解くのは非常に大変です。
今回の公式集では、因数分解のコツについても触れていきます。...
過去問演習

【過去問演習】多項式・整式の計算|数学Ⅰ【基礎】解説公式をまとめたら、大学・専門学校の問題を実際に解いてみましょう。
今回は多項式の計算について、基礎問題を紹介します。
僕の回...
ABOUT ME