2次方程式の解の公式は中学校でも教わるかと思いますが、改めて復習していきましょう。
また、2次方程式と解の配置も頻出問題ですが、グラフと軸の関係を描くことで思考を整理することができます。
解の公式について
- 解の公式
2次方程式 $ax^2+bx+c=0$ における実数解は
$x = \Large\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$ (ただし $b^2-4ac\geqq0$)
2次方程式の解き方
- 因数分解を試す
- ダメなら解の公式を使う
先ずは因数分解を試す
例 2次方程式 $x^2+3x+2=0$ を解くなら…
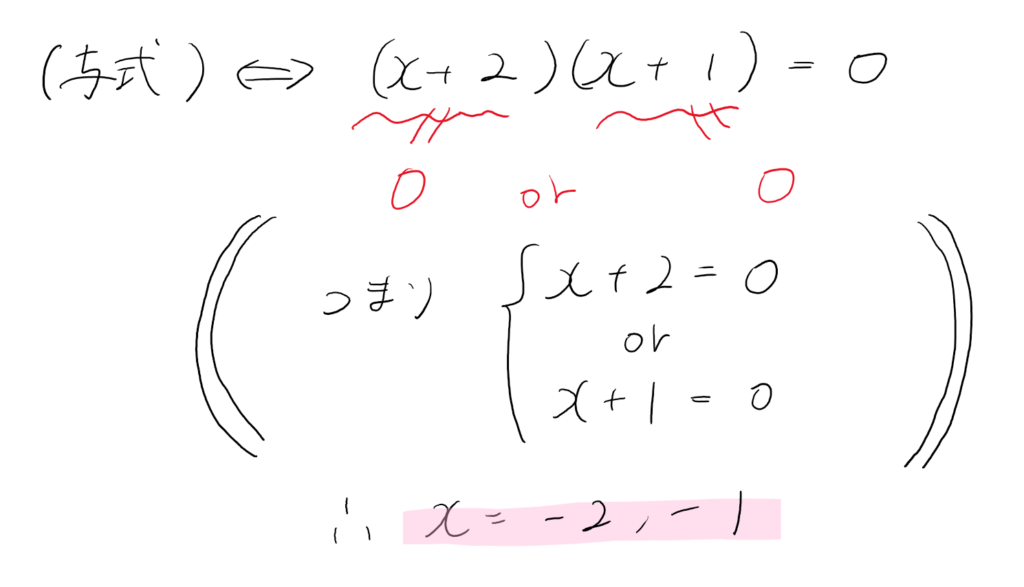
因数分解できないなら解の公式を使う
例 2次方程式 $x^2-4x+2=0$ を解くなら…

もし、ルートの中がマイナスになる(つまり $b^2-4ac\lt0$)なら計算ミスをしているか、解が実数解ではなく虚数解の可能性があります。
(虚数解については別の公式集にて扱います)
判別式について
- 2次方程式 $ax^2+bx+c=0$ における判別式 $D=b^2-4ac$
- 判別式の符号(または0になるか)によって解の個数が判別できる
- 重解:$D=0$ のとき解は1つ(2つの解が重なったと考える)
判別式 $D$ は、解の公式における√ の中身を意味します。
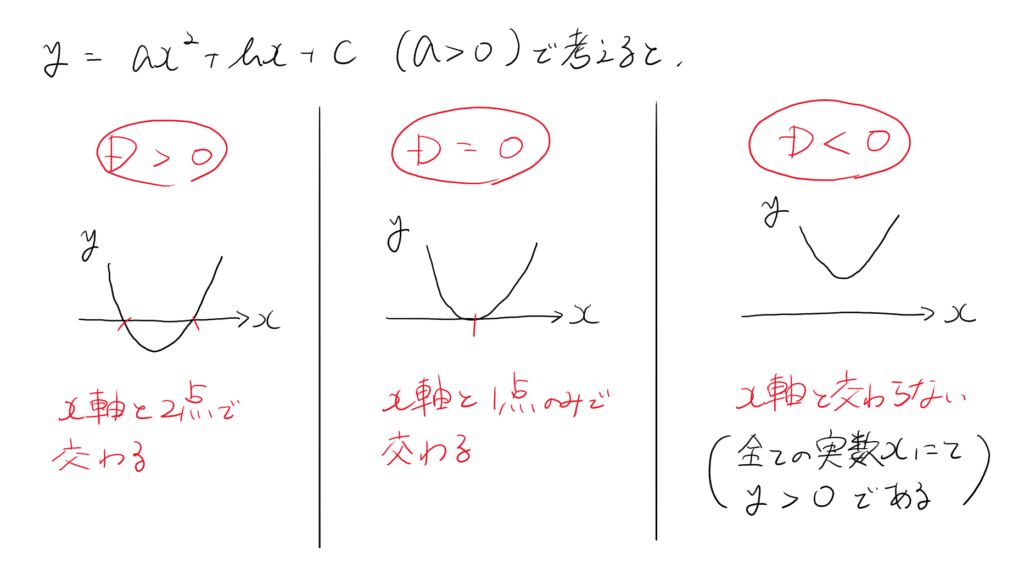
もし $a\lt0$ なら上図は $x$ 軸に対し対称移動して考えてください。
解と係数の関係
2次方程式 $ax^2+bx+c=0$ における2解が $\alpha, \beta$ なら…
- $\alpha+\beta=-\Large\frac{b}{a}$
- $\alpha\beta=\Large\frac{c}{a}$
2次不等式の解き方
- 両辺のグラフの上下関係を考える
ABOUT ME