【過去問演習】整式の展開・因数分解の計算｜数学Ⅰ【基礎】解説

$800\times700-801\times699$

$=800\times700-(800+1)(700-1)$

$=800\times700-(800\times700-800+700-1)$

$=101$

【解説】

$800\times700-801\times699$

（↓$801\times699$ を分解して計算を工夫）

$=800\times700-(800+1)\times(700-1)$

（↓分配法則で展開）

$=800\times700-(800\times700-800+700-1)$

$=800\times700-800\times700+800-700+1$

$=101$

$(2x-3)(2x+9)$

$=(2x)^2+2\times(-3+9)x-3\times9$

$=4x^2+12x-27$

$(x+2)(x+7)-x(x-9)$

$=x^2+(2+7)x+2\times7-(x^2-9x)$

$=18x+14$

$(x-3)(x+1)(x+3)(2x-2)$

$=(x+3)(x-3)\times(x+1)(2x-2)$

$=(x^2-9)\times(2x^2-2)$

$=2x^4-20x^2+18$

【解説】

$(x-3)(x+1)(x+3)(2x-2)$

（↓交換法則を用いて計算を工夫）

$=(x+3)(x-3)\times(x+1)(2x-2)$

$x+2=a$, $x+1=b$ とすると、

（与式）

$=(x+2)^3-(x+1)^3$

$=a^3-b^3$

$=(a-b)(a^2+ab+b^2)$

$a-b=(x+2)-(x+1)=1$ より、

（与式）

$=a^2+ab+b^2$

$=a^2-2ab+b^2+3ab$

$=(a-b)^2+3ab$

$=1+3ab$

$ab=(x+2)(x+1)=x^2+3x+2$より、

（与式）

$=1+3(x^2+3x+2)$

$=3x^2+9x+7$

【解説】

計算を簡単にするため、文字においてみた。

$a-b=1$ であることを上手く利用するために、基本対称式を利用して式を変形。

$6x^2-17xy+10y^2$

$=(x-2y)(6x-5y)$

【解説】

たすき掛けの公式を用いる。

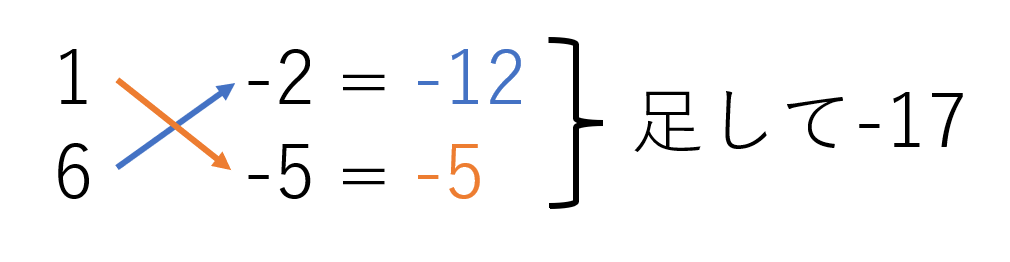
（因数分解した結果は、展開して検算をすることができる。）

$(x-y)^2-6(x-y)+9$

$=(x-y-3)^2$

【解説】

$x-y=t$ とすると、

（与式）

$=t^2-6t+9$

$=(t-3)^2$

$x^2+6xy+9y^2-x-3y-12$

$=(x+3y)^2-(x+3y)-12$

$=(x+3y-4)(x+3y+3)$