高校数学で最初に教わるであろう分野から公式集を作っていきます。
今回は、単項式・多項式・定数項などの用語についてです。
そもそもこれらの用語を知っていないと、先の分野で意味が分からなくなってしまうので、目を通す必要があります。
単項式・多項式とは
- 単項式:数や文字、それらを掛けただけで作られる式
- 多項式:単項式を足した式
例
$4$, $x$, $3ab^2$ などは単項式、
これらを足した $4+x+3ab^2$ は多項式です。
また、多項式における一つ一つの単項式を多項式の項と呼びます。文字の部分が同じ項を同類項といいます。同類項は係数の和を計算して、1つの項にまとめることができます。
整式と多項式の違いとは
整式:単項式と多項式の総称
つまり、単項式も多項式も整式です。
単項式を”項が1つの多項式”と考えると、多項式と整式は同じ意味になります。
なので、整式と多項式の違いは正確に言えばありますが、正直あまり気にしなくていいです。
定数項とは
定数項:多項式において着目している文字が掛けられていない項
パターン①
文字が1種類しかない多項式なら、文字のない数字が定数項です。
例 $x^2+2x+1$ なら…
文字のついていない $1$ が定数項。
パターン②
文字が2種類以上ある多項式なら、ある文字に着目して考えます。着目している文字が掛けられていない項が定数項です。
例 $ax^2+bx+c$ なら…
$x$ に着目すると、定数項は $c$ のみ。
基本的には、一番登場している文字(上式なら3回登場している$x$)に注目します。
係数・次数とは
係数と次数についても、定義を知っておくべきですので紹介します。
- 係数:単項式における数の部分
- 次数:単項式の数に掛けられた文字の数
例 単項式 $4x^2$ において
係数は $4$, 次数は $2$ です。
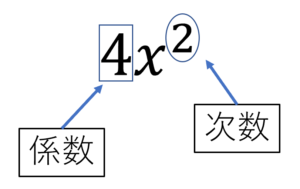
$x^2$ は $x$ を2回掛けているという意味ですからね。
ちなみに、ある文字に着目し、次数の高い項から順に並べていくことを、降べきの順に整理するといいます。
その整式、何次式?
n次式:最も高い次数がnの整式
例 $4x^3+3x^2+2x+1$ なら…
最も高い次数は $4x^3$ の次数 $3$ なので、3次式です。
過去問演習